|
The Binomial Distribution
The Binomial Distribution is used when an event has only two possible outcomes. Within the context of a series of trials these are generally called success and failure. The probabilities of each of these outcomes occurring are denoted by p and q respectively. Since the probability of a success is p, the probability of a failure is therefore ![]() . If an experiment is carried out with
. If an experiment is carried out with ![]() trials, the probability of
trials, the probability of ![]() successes (and consequently
successes (and consequently ![]() failures) is given by
failures) is given by
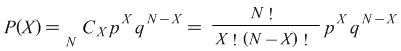
where ![]() N.B.
N.B. ![]() by definition. Because the binomial distribution was originally discovered by Jacob Bernoulli (1654-1705), it is sometimes called the Bernouilli distribution.
by definition. Because the binomial distribution was originally discovered by Jacob Bernoulli (1654-1705), it is sometimes called the Bernouilli distribution.
i) What is the probability of obtaining 4 heads out of 7 tosses of an unbiased coin?
Solution:
The tossing of a head is classed as a success. Consequently, the probability of 4 heads is given by
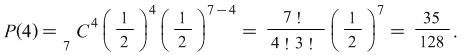
ii) What is the probability of dealing 2 spades if 6 cards are dealt from a normal pack of playing cards?
Solution:
The probability of dealing a spade is ![]() The probability of success (dealing a spade) and failure (not dealing a spade) are respectively
The probability of success (dealing a spade) and failure (not dealing a spade) are respectively ![]() and
and ![]() . Consequently, the probability of dealing 2 spades in 6 cards is given by
. Consequently, the probability of dealing 2 spades in 6 cards is given by
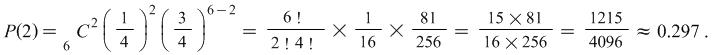
The mean, ![]() , of a binomial distribution is given by
, of a binomial distribution is given by ![]() .
.
The variance, ![]() , of a binomial distribution is given by
, of a binomial distribution is given by ![]() .
.
The standard deviation,![]() , of a binomial distribution is given by
, of a binomial distribution is given by ![]() .
.
Find the mean, variance and standard deviation for i) and ii) in the examples given above
Solutions:
i) ![]() . Consequently,
. Consequently, ![]() are given by
are given by
![]() ,
,
![]()
![]() .
.
ii) ![]() . Consequently,
. Consequently, ![]() are given by
are given by
![]() ,
,
![]()
![]() .
.
The moment generating function of the binomial distribution is given by
![]() .
.